My name is Proma Sen and I am a freshman at Macalester College, St. Paul, Minnesota. My major is yet undeclared but I have developed a keen interest in the subject of Economics.

My experience in math has been limited to whatever I have learnt through my years of schooling. I studied Math in the Indian system of education till year 10, after which I transferred to a UWC and took MATH HL as a part of the IB curriculum. I am not entirely sure what the weakest part of my Math background would be but I do remember struggling with infinite series for the IB. The strongest part of my Math background is probably Algebra and Trigonometry.

I am taking this Applied Calculus course because it is a pre-requisite for someone who wants to major in Economics. Through this course, I want to have a strong hold on the basics of understanding calculus, the math as well as why it can be relevant in today's world.

My interests are varied. I play the piano and the guitar. I sing in an a capella group on campus. I am heavily into music of all sorts but mainly old school rock. I used to play basketball in high school but have stopped since. I love watching football (soccer). I also like to read books outside of coursework when I get the time.

The worst Math teacher I ever had was in the 7th grade. My teacher would simply work out all the problems from the textbook on the board by herself and have us copy them down without any explanations. These were what we were to use as notes for the exam.

The best Math teacher I ever had was someone who always came up with entertaining everyday examples related to math and what she taught. Her quizzes were fairly challenging and it was a very competitive class but none the less enjoyable.

SECTION 1.2: Linear Functions

Linear functions are represented as straight line graphs. They may be increasing (olympic world record) or decreasing (a car decelerating) functions. These functions can be written in the form of y = f(x) = ax+b where

y is the value represented in the vertical axis of a graph (it is a function of x)
x is the value represented in the horizontal axis
b is the y-intercept of the graph (when x=0), and
a is the rate of change of y in relation to the change in x, i.e., it is the slope of the graph (slope= rise/run)

The reading section also identifies problems of extrapolation by which one tends to assume that the linear function demonstrates in the intervals in which the graph is drawn carry on endlessly. This may not always be the case. This depends on whether or not the data of the graph is discrete or continuous. Only a continuous function would continue to change at a constant rate on extrapolation.

The slope of the graph is a very important factor in understanding the function. The symbol delta is used to symbolize a change in values. Essentially, the slope, 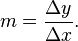which can also be written as 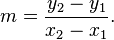This is defined as the difference quotient.

The equation of a line of slope m that passed through a point (x1,y1) can also be written as
y-y1= m(x-x1)

Note that a slope, m=0 implies that the function is a horizontal line, i.e., y=b.

Functions that share certain properties are defined as a family of linear functions. m and b are the parameters.

I personally found it challenging to differentiate between intervals of discrete data and continuous data.

The reading was very clearly relatable to Economics because I think functions, linear or otherwise, are important to all businesses when assessing their pros and cons of a financial decision with regard to the rate of change of fluctuating prices in the market.