Capstone Presentation:

The topic being studied at the presentation on Friday was Bisphenol A (hereby referred to as BPA), the chemical described as synthetic estrogen, present in many hard plastics found in everyday life especially bottles. There are many health risks to this organic chemical if it enters the body. It can potentially lower sperm count, result in sterilization as well as breast cancer. The current Canadian and U.S. limit of non harmful BPA consumption is 25 mg/ day.

The student who conducted the experiment aimed to test how long BPA would last in a fetus if consumed. She compartmentalized the body and used an ODE per compartment to model the flow of BPA in it. She derived a number of equations testing the dosage of BPA and the time in lasts in first body and thereby the fetus. She also used a physiological based pharmacokinetic model to test what the body does to the drug once its enters.

To graph the equations, she used Kawamoto et Al's model. She combined BPA as glucogen and the actual amount of drug in the body to plot a single line. She questioned whether BPA would disappear from a fetus over a period of time but she ultimately found that it remained at a constant rate within the fetus.

The student then took all her 27 equations from the compartmentalized study of the body and used varying toy model of bodies and fetuses to arrive at a single equation through nondimensionalization(i.e., making all main variables dimensionless).

The implications of her study were that BPA products should now be outlawed as it has been in Canada. Surprisingly enough baby bottles still cotain a significant amount of BPA in other parts of the world.

Through mathermatical modeling, the equations she arrived at concluded that a contstant low level of BPA will always remain in a fetus if injected at any given point in time. Also, doubling the dose of BPA will double the level of it remaining in the fetus.

I thought the study was very interesting and had a lot of relevant knowledge. The extrapolation of her data on the graph plotted bothered me a little, but someone asked the question in class and she seemed to prove it made sense even though i'm not entirely convinced. That is mainly because I didn't really understand the Kawamoto et Al's model used in the study.

SECTION 10.7: Modeling the spread of a disease

This section deals with the direct application of solving more than differential equation at the same time. It helps determine whether a disease is an epidemic or not and can help determined the level of vaccination necessary to prevent the disease.

Epidemics are studied based on an S-I-R model where S is the number of susceptible candidates for the sickness, I is the number of people already suffering from the disease and R is the number of people who have recovered from the disease. On the whole, in this model, it is assumed that the rate of change of susceptibles is related to th negative rate of change of the number of susceptibles who get sick. The rate of change of the number infected is the rate of change of susceptibles getting sick excluding the rate of change of those who have recovered.

( dS/dt= -aSI) and (dI/dt=aSI-bI) where a and b are constants. a measures how infectious the disease is and b represents the rate at which infected people are removed from infected population.

As a result of the above analysis, a threshold value is determined where the threshold population = b/a.

The section provides a very interesting study of exactly how calculus of this form can be directly applied in the field of science (especially biology). It could effectively help save lives when studied on a much larger scale.

SECTION 10.6: Modeling the Interaction of Two Populations

I understand that this section involves analyzing systems in which two differential equations are required in order to find a legitimate solution. But the reasoning for this has been using a phase plane of the two unknown variables studied in each differntial equations resulting in a slope field diagram and equillibrium points. As we have not yet studied slope fields in class, I was thoroughly confused in this reading. Beyond understand why the two equations are required in a situation such as the robin and the worm, I am unable to apply this concept to other real world situations because most of the solutions in this section don't make sense to me at this point. I apologize for the lack of detail in this blogpost but I geniunely don't understand the key points of this section!

SECTION 10.5: Applications and Modeling

In this section, derivatives related to the original equation with a difference of a constant A are taken into consideration, i.e., dy/dt = k (y-A), where k and A are constants.

Just as the solution to derivatives in the earlier section were found, the solution to the above mentioned derivative can also be determined.

If (y-A) is considered to be an exponential equation, then it must be in the form of C(e^kt).

Earlier we found that the exponential equation dy/dt = ky impliest hat y = C(e^kt). Therefore, this time the solution will vary by a constant A.

dy/dt = k(y-A) implies that y = A + C(e^kt) for any constant C.

Equilibirum solutions:

1. It is constant for all values of the independent variable. The graph is a horizontal line. They can be identified by setting the derivative of the function to zero.

2. It is stable is a small change in the initial conditions gives a solution which tends toward the equillibrium as the independent variable tends to positive infinity.

3. An equilibrium solution is unstable if a small change in the initial conditions gives a solution curve which veers away from the equilibrium as the independent variable tends to positive infinity.

This same principle is applied to Newton's law of heating and cooling by which

Rate of change in temperature = constant * Temperature difference.

This section although not directly applicable to economics is useful in understanding other everyday phenomenon. It is useful in the field of biology in order to know levels of drug concentration in a person. It is useful when solving murder cases or in hospitals when estimating times of death.

SECTION 10.4: Exponential Growth and Decay

A solution is defined as a function that is the same as its derivative. For example, an exponential function of the form e^x has a derivative equal to e^x. For an exponential equation, if the function contains a constant (k), the derivative of the function is a constant times the function, i.e., essentially the same as the original function. It implies that the rate of change of e^x is proportional to e^x where the constant k is the constant of proportionality.

The general equation for an exponential function is y = C(e^kt) where k is defines exponential growth if more than 0 and exponential decay if less than 0. The constant C is the value of y when t is 0. In a growth function expressing population, C would represent the initial population.

Exponential growth and decay can occur in many every day circumstances. It is relevant in the study of population growth, marine biology, pollution in cities, drug levels in people etc. My intended major still stands to be economics and so i am definitely aware through the book and other instances that learning to understand rates of change of derivatives functions whether those of exponential growth or decay are important to understand many aspects of banking (beyond just compund interest).

SECTION 10.2: Solutions of differential equations

A differential equation is formed when including the derivative of an unknown function. Its solution is any function that can be reduced to the differential equation/ satisfies it. The solution to the differential equation will be of numerical form and sometimes (if not always), the solution can be written as a another formula including a constant. To find the value for this constant, the initial value of unknown variable being studied needs to be known. Then substituting that value in the formula, we can find the constant.

A solution that satisfies a differential equation with a set initial condition is called a particular solution. The differential equation and the initial condition together is called an inital value problem.

This kind of information is useful in economics for a situation in which a person is aware of the rate of change of economic growth but needs to estimate more future values by formulating a general formula from the available derivative of unknown growth variable. This kind of theory is very important in understanding general trends of population growth etc. It is like moving backwards to find a general function when known the derivative.

SECTION 10.1: Mathematical Modeling: Setting up a differential equation

A differential equation is one that is formed based on the information on rates of changes of available values in the equation. This equation can then be analyzed in order to obtain the original function.

From the examples given in the textbook, it was observed that the rate of change of a certain quantity being study was effectively adjustable to the continuous rate of change of an increase or decrease of that quantity and the constant rate at which it is being increased or decreased. Assuming the Quantity being studied is Q,

dQ/dt = aX-Y where a determined the continuous rate of change and Y determines the constant rate of change. X would refer to the original value of the quantity being studied.

The Logistic Model:

The magnitude of a certain quantity being studied (e.g., population) is proportional to its initial value times the difference between its carrying capacity(the limit to which population in a town can increase) and the current value.

In other words if carrying capacity is L, the original and th original value is P then:

dP/dt = kP(L-P) where k is the constant of proportionality. This is known as a 'logistic differential equation'.

I found it difficult to understand exactly how the carrying capacity of a quantity as large as population can really be determined.

It is apparent that known how to use models with differntial equations assessing rates of changes can be important in assessing a company's revenues in terms of the changing wages it has to pay its workers. This section of mathematics is again directly relatable to economics.

SECTION 9.6: Constrained Optimization

Graphical Approach: Maximizing Production Subject to a Budget Constraint

If f(x,y) has a global maximum or minimum on the constraint g(x,y) = c, it occurs at a point where the graph of the constraint is tangent to a contour of f, or at an endpoint of the constraint.

Analytical Approach: The Method of Legrange Multipliers

If P0 is a point satisfying the constraint g(x,y) = c,
the function f has a local maximum at P0 subject to the constraint if f(P0) >= f(P) for all points P near P0 satisfying the constraint.
the function f has a global maximum at P0 subject to the constraint if f(P0) >= f(P) for all points P satisfying the constraint.

In this particular reading, I was thoroughly confused by the Lagrangian multiplier and the Lagrangian function. I couldn not blog properly on the reading as I couldnt not understand the significance of most of it.

It is however relevant to economics because budget constraints play a crucial role in the development of a firm at microlevel or an entire country's economy at the macrolevel.

SECTION 4.3: Global Maxima and Minima

The technique/ procedure for finding the global maximum or minimum in a graph is known as optimization. Local maxima or minima occur when a function takes larger or smaler values than nearby points.

A function f is said to have a global maximum at a if f(x) is <= all values of f. It is said to have a global maximum at a if f(x)>= all values of f.

To find the global maximum or minimum of a continuous function on an interval from point a to b, one must compare the values of the function at all critical points in the interval as well as the endpoints, i.e., a and b.

To find the global maximum and minimum of a continuous function on an interval excluding endpoints or on the entire real line, one must find the values of the function at al critical points and then sketch a graph through them.

SECTION 9.5: Critical Points and Optimization

Optimization means finding the largest or smallest values of a function. When interpreting graphs, the method of optimization is used to determine local or global maxima and minima.

A function f is said to have a local maximum at P0 if f(P0) >= f(P) for all points P near P0.
It is said to have a local minimum at Po if f(Po) <= f(P) for all points P near P0.

As explained above, the function has a global maximum at P0 if f(P0) >= f(P) for all points P in R and it has a global minimum at P0 if f(P0) <= f(P) at all points P in R.

If a function f(x,y) has a local maximum or minimum at a point (x0, y0) not in the limits of the domain of f, then either fx (x0,y0) = 0 and fy (x0,y0) = 0 or at least one partial derivative is undefined at the points (x0, y0). Points where each of the partial derivatives is either zero or undefined are called critical points. This is how a critical point of a function can be found analytically.

The part of these two reading sections I found difficult to understand was exactly how one can determine whether a critical point is a local maximum or minimum. The example of the function in the textbook was to confusing.

It is evident that understanding how to determine maximum and minimum poitns whether local or global is useful in economics and the business world because companies need to know how to maximize profits and minimize costs. These can in effect be determined by studying trends on a graph.

SECTION 9.3: Partial Derivatives

For a function. the influence of x and y is studied seperately on the value f (x,y) by keeping one variable fixed and varying the other. For all points (a,b):

The partial derivative of f with respect to x at (a,b) is the derivative of f with y constant.

fx (a,b) = rate of change of f with fixed y fixed at b, at the point (a,b) = lim h-0 ((f(a+(h,b)) - (f(a,b)))/ h

The partial derivative of f with respect to y at (a,b) is the derivative of f with x constant:

fy (a,b) = rate of change of f with x fixed at a, at the point (a,b) = lim h-0 ((f(a,b) + h) - (f(a,b)))/h

There is an alternative notation for Partial Derivatives:

If z = f(x,y) the we can say that,

fx (x,y) = dz/dx and fy (x,y) = dz/dy, where the d is more curvy than a regular derivative.

Partial derivatives can be used to estimate values of functions during research projects etc.

SECTION 9.4: Computing Partial Derivatives Algebraically

The second-order partial derivatives of z = f(x,y)

d^2(z)/ dx^2 = fxx = (fx)x

d^2(z)/ dxdy = fyx = (fy)x

d^2(z)/ dydx = fxy = (fx)y

d^2(z)/ dy^2 = fyy = (fy)y

It is to be noted that the mixed partial derivatives are equal, i.e., if fxy and fyx are continuous at (a,b) then fxy (a,b) = fyx (a,b)

SECTION 3.5: Derivatives of Periodic Functions

It is important to note that since sine and cosine functions are periodic, there derivatives must also be periodic. 

Graphically, it has been proven that if x is the radius,

d/dx(sin x) = cos x  and d/dx (cos x) = -sin x

If differentiating a function within a function, assuming the inside function is z and the outside function is sin or cos,

the d/dx (sin z) = cos z * (dz/dx)  and  d/dx (cos z) = - sin z * (dz/dx)

If k is a constant then,

d/dx (sin kx) = k *cos (kx)  and  d/dx (cos kx) = - k*sin (kt)

Again it is difficult to understand exactly why the following functions are applicable without seeing the theoretical proof for the derivations. But it will definitely be useful to know when working with differentiation of functions.

SECTION 3.4: The Product and Quotients Rule

The Product Rule:

If u = f(x) and v= g(x), and they are both differential functions then

(fg)' = f ' g + g ' f

It can also be written as :

d (uv)/ dx = (du/dx)*v + (dv/dx)*u

It is to be noted that the derivative of a product is not simply the product of the derivatives of the two functions involved. 

The Quotient Rule:

If u = f(x) and v = g(x)

then (f/g) ' = (f ' g - g ' f)/ g^2

It can also be written as d/dx(u/v) = ((du/dx)*v - (dv/dx)*u)/(v^2)

The difficulty in understanding this section lies in the usage of the quotient rule and how it was derived as essentially the function could simply be converted into a product rather than a quotient.

Derivatives continue to be important in analyzing smaller and smaller everyday changes. For this reason, both the product rule and the quotient rule serve to simplify the understanding of derivatives in everyday applicability.

SECTION 3.3: The Chain Rule

If y = f(z) and z = g(t), then the derivative of y = f(g(t)) is given as
dy/dt = dy/dz . dz/dt as long as dz and dt do not equal 0.

In other words, the derivative of a composite function s the derivative of the outside function times the derivative of the inside function:
d/dt f (g (t)) = f ' (g (t)) . g ' (t)

The chain rule can also be found for larger formulae by delaing with the formula as a single variable. For example,

y = (2t+1)^4 can be differntiated first by assuming a variable z = (2t+1)
Therefore, y = z^4
y' = 4(z^3)*z' = 4((2t+1)^3)*2 = 8(2t+1)^3

Some standard differential identities are as follows:
d/dt (t^n) = n*(t^n-1)
d/dt (e^t) = e^t
d/dt (ln t) = 1/t
d/dt (e^kt) = k*(e^kt) where k is an integer constant

Similarly,
d/dt (z^n) = n*(z^n-1)*dz/dt
d/dt (e^z) = (e^z)*dz/dt
d/dt (ln z) = (1/z)*dz/dt

I found it difficult to understand the example of how to determine the derivative of a composite function from a graph. I couldn't understand how it was being calculated. The theory made sense but the visuals didn't.

Again, learning how to determine rates of changes of irregular slopes over smaller and smaller intervals will always be useful in analyzing future market trends in a subject like Economics.

SECTION 3.2: Exponential and Logarithmic Functions

The Exponential Function:

The graph of an exponential function increases slowly for x<0>0. This implies that the derivative of a function f(x) = a^x, is small for x<0>0. Since the function is increasing for all values of x, the graph of the derivative always remains above the x-axis.

At a = 2.718... it is found that d/dx (a^x) = a^x. For this reason a is defined as the number e.
This implies that d/dx (e^x) = e^x.

The exponential rule of differentiation states that
d/dx (a^x) = (ln a)*(a^x)

Since ln a is a constant, it can be said that the derivative of the exponential function (a^x) is proportional to the original function.

The Derivative of Natural Logarithm:

The graph of f(x) = ln x, shows that ln x is always increasing. Therefore its derivative is positive. The graph of f(x) is concave down, therefore its derivative must be decreasing.

ln x is very large near x=0 and very small at x = infinity.

The natural logarithm rule of differentiation states that,
d/dx (ln x) = 1/x

The difficult part about this section was understanding exactly why those derivative formulae are obtained. Beyond seeing the graphical explanations, there isn't enough to really understand how ones arrives at those formulae.

Logarithms are another method used to interpret graphical trends and hence can be useful in Economics.

SECTION 3.1: Derivative Formulas for Powers and Polynomials

The derivative of constant is 0 as the slope of the line passing through that point is also 0.
Hence is f(x) = k, it implies that f ' (x) = 0.

The derivative of a linear function refers to the slope of that line, i.e.,
if f(x) = mx +b, f ' (x) = m

A function can be multiplied by a constant. If this is done, the general shape of the graph changes depending on the magnitude of the constant and its sign. The magnitude changes the slope of the curve at each point while the sign determines whether the function is reflected over the x-axis or not (reflected only if negative).
If c is a constant, then d/dx [c*f(x)] = c*f ' (x)

Derivatives of sums and differences of two functions can be found by simply adding or subtracting their magnitudes, i.e.,
d/dx [f(x) + g(x)] = f ' (x) + g ' (x) and,
d/dx [f(x) - g(x)] = f ' (x) - g ' (x)

Theoretically and graphically proven rules of differentiation:

The power rule:
d/dx (x^n) = n*[x^(n-1)]

The constant multiple rule:
d/dx [3*(x^5)] = 3*[d/dx(x^5)] = 3*[5*(t^4)] = 15(t^4)

The sum rule:
d/dx [(p^5)+(p^3)] = d/dx (p^5) + d/dx (p^3)

Similar rules can be used when differentiating to find the second derivative of a function. Finding the second derivative implies finding the derivative of the derivative of a function.

It is confusing to understand exactly what the graph of a second derivative aims to show of a function. It also brings up the question of whether a third or fourth derivative can also exist in a real world situation.

These formulae can be useful in determining general trends of markets. Anything related to graphs and relations of functions such as this can be useful in the field of economics.

SECTION 2.3: Interpretations of the Derivative

The derivative can be noted either as f ' (x) or delta y/ delta x

Leibniz took this to mean a small difference in y over a small difference x. 

dy/dx can also be regarded as the derivative of y with respect to x. It essentially defines a very very small change in y divided by an equally small change in x. 

It is important to note that the units of the derivative of a function are the units of the dependent variable (y) divided by the units of the independent variable (x). If the derivative of a function does not change rapidly near a point, then it is approximately equal to the change in the function when the independent variable increases by one unit. 

An example of an everyday use of the derivative:

Derivative of velocity = dv/dt = acceleration, the units of which are meters per second squared.

Derivatives can also be used to estimate values of functions, i.e., the change in value of dependent quantity with every unit increase in independent quantity. In other words, local linear approximation can be found by using delta y = f ' (x) * delta x. 

I found it difficult to understand exactly at which point, the value of the derivative would be most accurate. As all values calculated seem to be approximations, what defines their accuracy and to how many decimal places?

This section is useful in Economics because understanding the unit changes if quantities is very  important. Marginal costs or benefits are always important when making big decisions. For example, to understand whether hiring one additional person to the labour force increases a firms efficiency/ profits or not. 

SECTION 2.2: The Derivative Function

The derivative of a function can be estimated graphically by finding the slope of the tangent to a point on a graph. This is so because, in general, the derivative function f '(x) is defined as the instantaneous rate of change of f at x.

Graphically, the derivative graph tells us that,
if f ' > 0, then f is increasing
if f ' < 0, then f is decreasing and
if f ' = 0, then f is constant.

Note: If the magnitude of f ' is large then the graph of the derivative is steep. Conversely, if the magnitude if small, the graph is gently sloping.

A derivative can also be obtained/ estimated from a table of data by finding the change in the x values of the data and dividing it by the change in y values of the data. Essentially, this implies finding the slope of the data when graphed.

Derivatives of certain points can also be numerically estimated by studying the average of rates of changes of point to the left and to the right of it.

What I found confusing in this reading, was the suggestion that derivatives of points could also be numerically calculated by just analyzing points to the right of it.

This reading was very useful in economics as learning derivatives in general helps understand market situations relating to recessionary, inflationary or other phases of the business cycle. For example when f ' = 0, it would imply that the market is going through a lull/ no activity phase.

SECTION 1.3: Rates of Change

Rates of Change can be calculated in a similar way to the slope of a linear function, as analyzed earlier. The rate of change of a non-linear function is determined as an average.
If a function y = f(t),
then the average rate of change of y = change in y/ change in t = f(b)-f(a)/ (b-a),
assuming that the rate is being calculates between an interval of t=a and t=b.

Rates can be positive or negative. They help determined whether a function is increasing or decreasing. Increasing functions have positive rates and decreasing functions have negative rates. A function is said to be increasing if the values of f(x) increase as x increases. Similarly, a function f is said to be decreasing if the values of f(x) decrease as x increases.

Rates of change can be easily visualized:

The change in y refers to the vertical change of the graph while the change in x refers to horizontal change of the graph over a period of time. In the diagram below, the change in y between the two demarcated points would be approximately (90-50) while the change in x would be (0-(-10)).


The shape of a graph can also be determined by its concavity. A graphs that bends upwards from left to right is called concave up while a graph that bends downwards is considered to be concave down. The graph above is an example of a concave up graph.

Everyday rates that we encounter include velocity and speed, i.e.,

Average velocity = change in displacement/change in time while,

Average speed = change in distance/ change in time

SECTION 2.1: Instantaneous Rate of Change

To calculate velocity to exact accuracy required, smaller and smaller intervals on either side of the time taken can be determined until the average velocity agrees to the number decimal places needed. This can also be expressed as instantaneous velocity.

Instantaneous velocity is defined for an object at time t as the limit of the average velocity of the object over shorter and shorter time intervals containing t.

To look at a more general idea of the above states reasoning, instantaneous rate of change of a function at say, t, is also called the rate of change of f at t. It is defined as the limit of the average rates of change of f over shorter and shorter intervals around a. This instantaneous rate of change is also referred to as the derivative of f at point a and is written as f '(a).

The derivative of a function is essentially the slope of the function at a or the slope of the line tangent to the curve at a. Similar to the rate of change, a derivative can be positive or negative thereby determining whether the function is increasing or decreasing.

What I found challenging about these sections was deciphering whether or not having a rate of change still indicated a slope between the two points despite the fact that the graph was not linear.

The concept of average rates of change is always useful in everyday situations as not all relationships between values can be of a linear form.

SECTION 9.1: Understanding Functions of Two variables

To indicate that a certain result is dependent on two variables we say that R = f(x,y) where
R is the dependent variable
x and y are the two independent variables and
f stands for "function".

All combination of values of (x,y) are called the domain of f. It is said that a function is increasing(decreasing) if one of its variables simultaneously increases(decreases) as the other is held constant.

The combination of x and y variables can be represented in the form of a table. From this table an algebraic formula can be derived. This is usually written in the form of R = ax + by, where a is the amount by which each additional quantity of x changes and b is the amount by which each additional quantity of y changes. We can then also say that R = f (x,y) or f (a,b).

A way to investigate functions of two variables/ quantities dependent on two variables, one cab vary one variable over a period of time while keeping the other constant and vice versa. The change in one variable compared to the other can easily be graphed and hence interpreted in a way in which one can understand the effect of a variable more clearly as the other remains constant.

SECTION 9.2: Contour Diagrams

Functions of two variables can also be expressed as diagrams known as contours or level curves/ level sets. Such diagrams are put to use in everyday situations while deciphering weather conditions through isotherms and by studying topographical maps depicting mountains, valleys, ridges etc.

For the latter, closer lines imply mountain regions while the ones further apart usually refer to plains. The elevation numbers on the contours are important because they represent the curves of the mountains themselves. In general, contours marked in constant intervals and spaced closely together usually depict steeper terrain.

The one important point to keep in mind is that contours can never intersect.

Contour diagrams function in exactly the same way as other algebraic two variable functions. The values through the x and y values from contours can also be depicted in the form of a table if required to do so.

Cobb-Douglas Production Functions:

These are often used by businesses to estimate how revenue can be maximized through various production possibility levels (for example, whether they should initiate growth by increase number of laborers or number of machines). The graph usually looks as following:



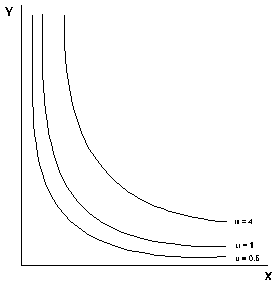
The function is written as P = f (N,V) = c(N^alpha)(V^beta) where,
P is the total quantity produced,
and c, alpha and beta are positive constants (alpha and beta lie between 0 and 1)

I had difficulty understanding why the production model has the shape it does... in fact I'm still not exactly sure why that is.

It is evident that the Cobb-Douglas Production Function is relevant to Economics Majors because it helps businessmen anticipate the results of their decisions by weighing the opportunity costs of making one decision over another.

SECTION 1.10: Periodic Functions

Functions that have values occurring at regular intervals are known as periodic functions. Many everyday processes can be referred to as periodic for example, the temperature in a day rise all the way till noon, begins to fall as night approach, and repeats the same pattern every single day.

Amplitude of a periodic wave is the average difference between the maximum and minimum values, i.e., A = (max-min/2). The period of the wave is the time it takes to complete one oscillation/cycle.

To important periodic functions to be studied are the sine and cosine functions. Their graphs are equally important. It is to be noted that the graph of the cosine function is the graph of the sign function, shifted pi/2 to the left.

The graph for sin(x) looks as follows:



As can be seen it has an amplitude of 1 and a period of 2(pi).

The graph for cos(x) looks as follows:



As can be seen, it has an amplitude of 1 and a period of 2(pi) as well.

For an expression of a sine or cosine curve where

y = Asin(Bx+C)+D or y = Acos(Bx+C)+D

A affects the amplitude of the curve. Infact the absolute value of A is the amplitude of the curve.
B affects the period, i.e., period = 2(pi)/absolute value of B.
C affects the horizontal shift of the curve, and
D affects the vertical shift.

The part of graphing such sine and cosine curves that I found most challenging was when determining the amount by which and the direction in which curves moved when experiencing a horizontal shift. The positive and negative signs of C were slightly confusing.

Again, as mentioned before, periodic functions are extremely related to Economics because of business cylces are usually recurring phenomenon, i.e., periodic functions of recessions and booms. Hence the ways in which the operate is directly related to the shifts experienced by a regular sine or cosine function.

SECTION 1.9: Proportionality, Power Functions, and Polynomials

When a quantity y is proportional to a quantity x, then it is implied that y = kx where k is described as the constant of proportionality (the number of times by which quantity y changes with change in quantity x).

The quantities are said to be directly proportional when the increase (decrease) in value of one results in the increase (decrease) in value of the other.

The quantities are said to be inversely proportional if one quantity is proportional to the reciprocal of the other. This implies that the increase in one quantity results in a decrease in the other quantity and vice versa.

For example, to say velocity = displacement/ time indicates that velocity is directly proportional to displacement and inversely proportional to the quantity time.

It is said that y is a power function of x if y is proportional to a constant power of x, i.e., y = k(x^p), where k is still the constant of proportionality and p is the power.

Some graphs of basic power functions can be explored: It is seen the (x^2) is consistently concave up. Values of y decrease for -x and increase for +x. The graph of (x^3) is concave down for all values of -x and concave up for all values of +x. The graph of (x^1/2) is increasing and concave down.

Sums of power functions with non-negative integer expoenets are called polynomials. They can be written in the following form:

y = an*(x^n) + an-1*(x^n-1) + ... + a1*x + a0

where,
n is a non-negative integer called the degree of the polynomial
an is a non-zero number called the leading co-efficient, and
an*(x^n) is called the leading term.

If n=2, the polynomial is quadratic.
If n=3 the polynomial is cubic.
If n=4, the polynomial is quartic
If n=5, the polynomial is quintic and so on.

Personally, I find it challenging to graph polynomials especially when they get more complicated (as in fractions) and their asymptotes are not as obvious.

The relevance of such polynomials and the concept of proportionality is extremely important in Economics to understand the fluctions in the demand and supply with changes in price of goods. The price at which maximum revenue can be attained also depends on the kind of relationship between the good and the people's demand for it. Also, demand for complementary goods is dependent on the concept of direct proportionality as is the demand for substitute goods dependent on the concept of inverse proportionality.

SECTION 1.7: Exponential Growth and Decay

Many functions can be defined in the form of P = P0 (e ^kt) where P0 is still defined as the initial quantity and k is the continuous growth or decay rate. When k is negative it represents a decay. When it is positive it refers to exponential growth. "e", as mentioned in the previous post, is defined as a natural base.

Two new concepts defined in this sections were doubling time and half-life:

Doubling time of an increasing exponential function is the time required for the quantity to double itself.

Half- life of a decaying exponential function is the time required for the quantity to be reduced to half its current amount.

All growing functions have a doubling time, and all decaying functions have a half-life.

Compound interest on an amount saved in a bank can be defined exponentially. If an initial
amount of P0 is deposited in a bank that has an interest rate of r/ year, assuming P is the balance in the bank over t years, it can be said that
- interest compounded annually implies P = P0 (1+r)^t
- interest conpounded continuously implies P= P0(e^rt) where e is again the natural base.

In business terminology, there are two important terms to remember:

The future value of an amount P is the amount to which P will grow in an interest-bearing bank account.

The present value, P, of a future payment is an amount that will have to be deposited in a bank now to produce the amount of future payment at the relevant time.

In this reading, I was confused by the term 'interest compounded continuously' because I could not easily understand how this could happen when the interest rate itself was defined per year.

It is clearly seen that this section of exponential functions is most related to Economics. Interest rates are crucial to bankers, borrowers and lenders. Understanding how one's savings grow in a bank is equally important and necessary in managing one's own finances.

SECTION 1.5: Exponential Functions

If the percentage increase or decrease in a quantity is a constant, then the function is defined as an exponential function. Population growth in certain areas is an example often used for demonstrating exponential growth.

Exponential functions are defined as P = P0 (a^t) where
P represents the vertical axis of a graph
P0 represents the initial quantity (when t=0), and
a represents the the factor by which the function increases or decreases. It is called a base.
If a>1, there is said to be exponential growth, if a<1, there is said to be exponential decay. Larger values of a imply faster growth. and values of a near 0 im
ply faster decay.
It can also be written as a = 1+r, where r is the decimal representation of the percent rate of change. It is positive for exponential growth and negative for exponential decay.

For an exponential decay to occur, as t increases the functions values get closer and closer to zero. Therefore the t-axis represents the horizontal asymptote of the function.

It is also important to note that graphs of exponential functions are always concave up.

To differentiate between an exponential function and a linear function, it is important to understand that the former refers to a constant relative rate of change while the later refers to an absolute value for the rate of change.

In everyday situations the most common base number is defined as e= 2.71828... This is often called the natural base.

When reading this section, the question that arose in my mind was whether or not the base a could be a negative number, and if not then why?

This material was relevant to what had been studied in the earlier section, especially in discussing why certain data when extrapolated beyond certain intervals could still be considered functions and yet not change at a constant absolute rate. The section helped clearly identify the differences between linear and exponential functions.

My name is Proma Sen and I am a freshman at Macalester College, St. Paul, Minnesota. My major is yet undeclared but I have developed a keen interest in the subject of Economics.

My experience in math has been limited to whatever I have learnt through my years of schooling. I studied Math in the Indian system of education till year 10, after which I transferred to a UWC and took MATH HL as a part of the IB curriculum. I am not entirely sure what the weakest part of my Math background would be but I do remember struggling with infinite series for the IB. The strongest part of my Math background is probably Algebra and Trigonometry.

I am taking this Applied Calculus course because it is a pre-requisite for someone who wants to major in Economics. Through this course, I want to have a strong hold on the basics of understanding calculus, the math as well as why it can be relevant in today's world.

My interests are varied. I play the piano and the guitar. I sing in an a capella group on campus. I am heavily into music of all sorts but mainly old school rock. I used to play basketball in high school but have stopped since. I love watching football (soccer). I also like to read books outside of coursework when I get the time.

The worst Math teacher I ever had was in the 7th grade. My teacher would simply work out all the problems from the textbook on the board by herself and have us copy them down without any explanations. These were what we were to use as notes for the exam.

The best Math teacher I ever had was someone who always came up with entertaining everyday examples related to math and what she taught. Her quizzes were fairly challenging and it was a very competitive class but none the less enjoyable.

SECTION 1.2: Linear Functions

Linear functions are represented as straight line graphs. They may be increasing (olympic world record) or decreasing (a car decelerating) functions. These functions can be written in the form of y = f(x) = ax+b where

y is the value represented in the vertical axis of a graph (it is a function of x)
x is the value represented in the horizontal axis
b is the y-intercept of the graph (when x=0), and
a is the rate of change of y in relation to the change in x, i.e., it is the slope of the graph (slope= rise/run)

The reading section also identifies problems of extrapolation by which one tends to assume that the linear function demonstrates in the intervals in which the graph is drawn carry on endlessly. This may not always be the case. This depends on whether or not the data of the graph is discrete or continuous. Only a continuous function would continue to change at a constant rate on extrapolation.

The slope of the graph is a very important factor in understanding the function. The symbol delta is used to symbolize a change in values. Essentially, the slope, 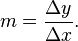which can also be written as 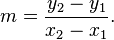This is defined as the difference quotient.

The equation of a line of slope m that passed through a point (x1,y1) can also be written as
y-y1= m(x-x1)

Note that a slope, m=0 implies that the function is a horizontal line, i.e., y=b.

Functions that share certain properties are defined as a family of linear functions. m and b are the parameters.

I personally found it challenging to differentiate between intervals of discrete data and continuous data.

The reading was very clearly relatable to Economics because I think functions, linear or otherwise, are important to all businesses when assessing their pros and cons of a financial decision with regard to the rate of change of fluctuating prices in the market.